28.75We are asked to determine the volume of a hemisphere of diameter 28 3/4 in.
A hemisphere is half a sphere therefore, its volume is half the volume of a sphere:
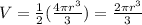
Where "r" is the radius. Since the radius is half the diameter we have that:
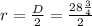
We will convert the mixed fraction into a standard fraction using the following:
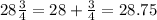
Substituting in the formula for the radius:
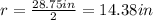
Now, we substitute the value of the radius in the formula for the volume:
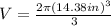
Solving the operations:
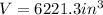
Therefore, the volume is 6221.3 cubic inches.