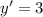Question

Find the derivatives of the following using the different rules.1. y = 3x + 29

Answer 1

To find the derivative of the given function, we can use the power rule.

`ax^n\Rightarrow nax^(n-1)`

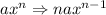
In this rule, we multiply the exponent of the variable by its numerical coefficient and then subtract 1 from the exponent.

For this function y = 3x + 29, we have two terms. These are 3x and 29. We need to apply the power rule for each term.

Let's start with 3x.

`3x^1\Rightarrow1(3)(x^(1-1))\Rightarrow3x^0\Rightarrow3`

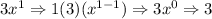
The first derivative for 3x is 3.

For the term 29, since there is no variable, the derivative for 29 is 0.

So, the first derivative of y = 3x + 29 is y' = 3 + 0 or just y' = 3.

`y^(\prime)=3`