Answer:
• D=249
,
• Two real numbers zeros
Step-by-step explanation:
Given the quadratic function:
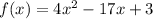
a=4, b=-17, c=3
The discriminant is obtained using the formula:
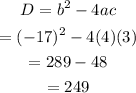
Since the discriminant is greater than 0, the equation has 2 real solutions (or zeros).
Note:
• If D<0, the equation has 0 real solutions.
,
• If D=0, the equation has 1 real solution.