In this case, the order doesn't matter and the colors cant be repeated.
Now, we need to use the permutation formula:
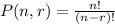
Where n represents the total different available colors and r is equal to
the number of doors.
Replacing on the permutation formula:
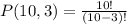
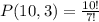
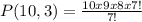
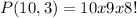
Then
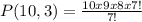
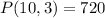
Hence, there are 720 possible arrangements for the doors.