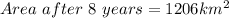Question

A certain forest covers an area of 2300 km^2. Suppose that each year this area decreases by 7.75%. What will the area be after 8 years?Use the calculator provided and round your answer to the nearest square kilometer.

Answer 1

Step-by-step explanation:

Given;

We are told that a forest covers an area of 2300 square kilometers.

Next we are told that this forest area decreases by 7.75% each year.

Required:

We are required to calculate the area remaining after 8 years.

Step-by-step solution:

To solve this math problem, take note that what we have is an exponential decay problem. The initial size decreases (decays) at a constant rate every year.

The formula for an exponential growth/decay is given as shown below;

`f(x)=a(1-r)^x`

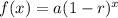
Where the variables are as follows;

`\begin{gathered} a=initial\text{ }value \\ r=rate\text{ }of\text{ }decay \\ x=number\text{ }of\text{ }years \end{gathered}`

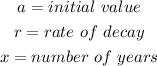
With the values given, we can substitute and we'll have the following;

`f(8)=2300(1-0.0775)^8`
`f(8)=2300(0.9225)^8`
`f(8)=2300(0.524482495947)`
`f(8)=1206.3097...`

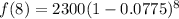
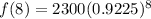
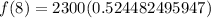
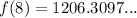
Rounded to the nearest square kilometer, we would now have;

ANSWER:

`Area\text{ }after\text{ }8\text{ }years=1206km^2`