Question

Can someone please help I've gone through 4 different teachers

Answer 1

Answer:

a) see graph below

b) The coordinate of F" = (12/13, 0)

c) cos(D") = 12/13

sin(D") = 5/13

tan(D") = 5/12

Step-by-step explanation:

Given:

A triangle on a coordinate with the units on the vertical and horizontal axis unlabeled

To find:

To label the diagram D"E"F" and determine the coordinates of F"

To label the diagram, we will use the previous diagrams and solutions.

From the information given, the new diagram is similar to the triangle DEF

For similar triangles, the ratio of their corresponding sides will be equal. Also, the corresponding angles are also equal

This means D corresponds to D", E corresponds to E" and F corresponds to F"

labeling the diagram:

b) To get the coordinates of F', we will use the similarity theorem about ratio of corresponding sides:

we have the hypotenuse = 1

the adjacent or base = not given

To get the base, we will use cosine ratio (CAH)

cos D" = adj/hyp

let the adjacent = b

cosD" = b/1

From previous solution of cos D and cos D', the result was 12/13

equating the ratio:

`\begin{gathered} cosD^(\prime)^(\prime)\text{ = }(b)/(1)\text{ } \\ cos\text{ D = 12/13} \\ cos\text{ D = cos D'' \lparen similarity theorem\rparen} \\ (b)/(1)\text{ = }(12)/(13) \\ b\text{ = 12/13} \end{gathered}`

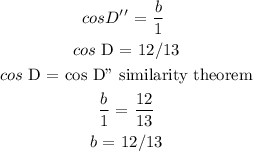
This means the x coordiante of E" = 12/13

Next, we will find the opposite

sin D" = opp/hyp

sinD'' = opp/1

sin D = 5/13

sin D = sin D" (similarity theorem)

`\begin{gathered} (5)/(13)=(opp)/(1)\text{ } \\ opp\text{ = 5/13} \end{gathered}`

The coordinates of D"E"F":

The coordinate of F" = (12/13, 0)

How: This was determined using the similarity theorem. Comparing the ratio of the corresponding sides of triangle DEF with triangle D"E"F".

cos(D") , sin(D") and tan(D") will have same value as cos (D), sin(D) and tan (D) respectively.

This is because they are similar triangles and the corresponding angles in similar triangles are equal

cos(D") = 12/13

sin(D") = 5/13

tan(D") = 5/12