Question

3. 1.819 m4. 5.291 m5. 6.321 m39. Answer: B40. Work done by the non conservative forces actingon an object is equal1.to the change in the mechanical energy of the object2. to the change in the kinetic energy of the object3. to the work done by the conservative forces4. to the change in the potential energy of the object5. to the net work done on the object41. Answer: A

Answer 1

We are asked to determine the distance that spring will stretch when a given mass is attached to it.

To do that we will use Hook's law:

`F=kx`

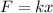
where:

`\begin{gathered} F=\text{ force } \\ k=\text{ spring constant} \\ x=\text{ distance that the spring is stretched} \end{gathered}`

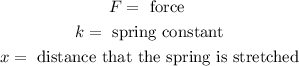
We will determine the constant of the spring "k" first using the fact that the spring is stretched 0.8 meters when a mass of 3kg hangs from it.

Since the only force acting on the spring is the weight of the object we have:

`F=mg`

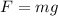
Where:

`\begin{gathered} m=\text{ mass} \\ g=\text{ acceleration of gravity} \end{gathered}`

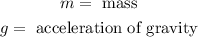
Now, we substitute and we get:

`mg=kx`

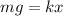
Now, we divide both sides by "x":

`(mg)/(x)=k`

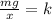
Now, we plug in the values:

`((3kg)(9.8(m)/(s^2)))/(0.8m)=k`

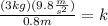
Solving the operations:

`36.75\text{ N/m}=k`

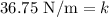
Now, we substitute the value of "k":

`F=(36.75\text{ N/m\rparen}x`

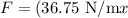
Now, we solve for "x":

`\frac{F}{36.75\text{ N/m}}=x`

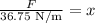
Now, we substitute the value of the weight of the second object:

`\frac{(14kg)(9.8(m)/(s^2))}{36.75\text{ N/m}}=x`

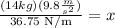
Solving the operations:

`3.733m=x`

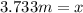
Therefore, the spring will stretch by 3.733 meters.