The three tents form a triangle with two sides given by the distances between your tent and the tents of your friends; the remaining side is the distance between Joe's and Karl's tents.
To determine this side (and hence this distance) we need to notice that the angle between the two known sides is the addition of the angles between those sides and your position, hence the angle between the sides is 62°.
Now that we know this we can use the cosine law to determine the distance between the tents. The cosine law states that:
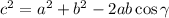
this means that the squared of the distance we are looking for is equal to the sum of the squares of the other two distances minus twice the product of the other two sides and the cosine of the angle between them.
Then we have that:
![\begin{gathered} c=\sqrt[]{21.5^2+44.5^2-2(21.5)(44.5)\cos (62)} \\ c=39.3 \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/f1u3rrr2e7g6npcjy7rpiqx042r26gops8.png)
the distance we are looking for is the square root of twenty one point five squared plus forty four point five squared minus two multiplied by twenty one point five by forty four point five by the cosine of 62.
By making the operations we conclude that the distance between Joe's and Karl's tents is thirty nine point three meters