Given:
The length of the slinky is: L = 4 m.
The time taken by the wave to travel the length and back again is: t = 4.97 s
To find:
a) The speed of the wave
b) The frequency of the wave
Step-by-step explanation:
a)
As the wave on the slinky travels along the length and back again, it covers a distance that is double the distance of the slinky.
Thus, the total distance "d" traveled by the wave will be 2L.
The speed "v" of the wave is given as:
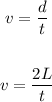
Substituting the values in the above equation, we get:
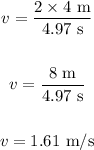
Thus, the speed of the wave is 1.61 m/s
b)
The standing wave created consists of seven antinodes and eight nodes. Thus, the length of the slinky is 7/2 times the wavelength of the wave.
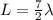
Rearranging the above equation, we get:
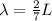
Substituting the values in the above equation, we get:
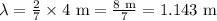
The speed "v" of the wave is related to its wavelength "λ" and a frequency "f" as:
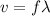
Rearranging the above equation, we get:
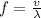
Substituting the values in the above equation, we get:
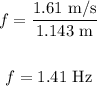
Thus, the frequency of the wave on the slinky is 1.41 Hz.
Final answer:
a) The speed of the wave is 1.61 m/s.
b) The frequency of the oscillation of the slinky is 1.41 Hz.