Question

Question 4Task 2: Nee how (hello)Business is projected to be booming after the latest release of The Fast and the Furious3.14159265359... Carver's Auto Custom must determine how many cans of paint and rims tostock at their Shanghai location.The Carver Family did choose Warehouse Space A. The warehouse includes 8000 sq. ft. ofshowroom and workshop space. One half of this warehouse space will be used to stock paintcans and rims. The warehouse has a height of 20 ft.Tell how many of cans you will stock. You must have exactly 4 cans ofpaints for every rim you stock.

Answer 1

The area of the warehouse is

`A=8000ft^2`

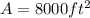
Half of this area stock paint, cans and rims:

`\begin{gathered} A_{\text{stock}}=4000ft^2 \\ \text{then, the volume of the room is} \\ V_{\text{stock}}=4000*20 \\ V_{\text{stock}}=80000ft^3 \end{gathered}`

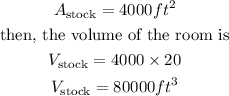
thats because the heigth of the stock room is equal to 20 ft.

On the other hand, we know that there are 2 cans in a box which volume

`\begin{gathered} V_{\text{box}}=15*7*6inches^3 \\ \text{then for one can, the volume is} \\ V_{\text{can}}=(V_(box))/(2)=(15*7*6)/(2)=15*7*3inches^3 \\ V_{\text{can}}=315in^3 \end{gathered}`

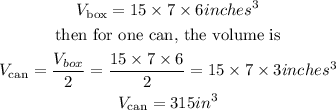
and a rim is inside a box with measures

`\begin{gathered} V_{\text{rim box}}=36*36*15inches^3 \\ V_{\text{rim box}}=19440in^3 \end{gathered}`

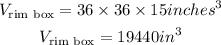
Then, we need to find the ratio V_total to V_stock in order to find the number of rims in the room.

Then, V_total is the sum of 4 times the volume of one can plus the volume of 1 rim, that is,

`V_{\text{total}}=4\cdot V_{\text{can}}+V_{\text{rim}}`

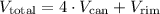
because we need 4 cans and 1 rim in our room. This total volume is given by

`V_{\text{total}}=4\cdot315+19440inches^3`

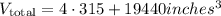
which gives

`V_{\text{total}}=20700inches^3`

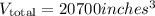
The last step is convert the V_total from cubic inches to cubic feets. We can do that by means of

`V_{\text{total}}=20700inches^3((1ft^3)/(12^3inches^3))`

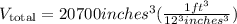
because 1 feet is equal to 12 inches. It yields,

`\begin{gathered} V_{\text{total}}=20700((1)/(144)) \\ V_{\text{total}}=143.75ft^3 \end{gathered}`

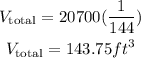
Finally, we can find the ratio mentioned above:

`\text{ratio}=(V_(stock))/(V_(total))=(80000)/(143.75)=556.52`

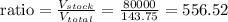
By rounding down to the nearest interger, the ratio is 556. This means that we can stock 556 rims in the warehouse.