Question

John wishes to build a square fence with an area of 121 square yards. What is the perimeter of the fence in yards.

Answer 1

Given that John wishes to build a square fence with an area of 121 square yards, as shown below:

The area of a square is expressed as

`\begin{gathered} Area\text{ of square = L}^2 \\ where \\ L\Rightarrow length\text{ of a side of the square} \end{gathered}`

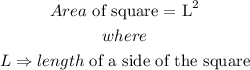
Given that the area of the square fence is 121 square yards, this implies that

`\begin{gathered} 121=L^2 \\ take\text{ the square root of both sides,} \\ \sqrt{121\text{ }}\text{ =}√(L^2) \\ √(11*11)\text{ =}√(L* L) \\ \Rightarrow L=11\text{ yards} \end{gathered}`

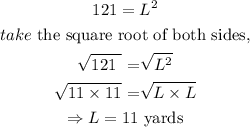
The perimeter of a square is expressed as

`\begin{gathered} Perimeter\text{ of square = 4}* L \\ where \\ L\Rightarrow length\text{ of a side of the square} \end{gathered}`

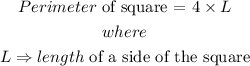
Thus, the perimeter of the fence is evaluated by substituting the value of 11 for L into the perimeter formula.

`\begin{gathered} Perimeter\text{ of fence = 4}*11 \\ \Rightarrow Perimeter\text{ of fence = 44 yards} \end{gathered}`

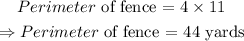
Hence, the perimeter of the fence is 44 yards.