We are given the following system of equations:
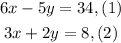
We are asked to verify if the point (-36, 58) is a solution to the system. To do that we will substitute the values x = -36 and y = 58 in both equations and both must be true.
Substituting in equation (1):

Solving the left side we get:
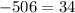
Since we don't get the same result on both sides this means that the point is not a solution.
Now, we will determine where was the mistake.
The first step is to solve for "y" in equation (2). To do that, we will subtract "3x" from both sides:

Now, we divide both sides by 2:
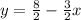
Solving the operations:
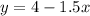
Now, we substitute this value in equation (1), we get:
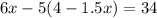
Now, we apply the distributive law on the parenthesis:

This is where the mistake is, since when applying the distributive law the product -5(-1.5x) is 7.5x and not -7.5x.