Question

A veterinarian is enclosing a rectangular outdoor running area against his building for the dogs he cares for (see image). He wants to maximize the area using 108 feet of fencing.

Answer 1

The width that will give the maximum area is 27 feet. The maximum area is 1458 square feet.

Step-by-step explanation

The equation that gives the area is a quadratic function,

`A(x)=x(108-2x)`

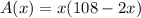
To find the width that maximizes the area, we have to find the x-coordinate of the vertex of this parabola. We can observe in the equation that the leading coefficient is -2, so the vertex is the maximum.

First, apply the distributive property to write the equation in standard form,

`A(x)=-2x^2+108x`

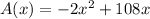
The x-coordinate of the vertex of a parabola if the equation is in standard form is,

`\begin{gathered} y=ax^2+bx+c \\ \\ x_(vertex)=(-b)/(2a) \end{gathered}`

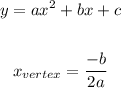
In this case, b = 108 and a = -2,

`x_(vertex)=(-108)/(-2\cdot2)=(108)/(4)=27`

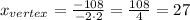
Hence, the width that will give the maximum area is 27 feet.

To find the maximum area, we have to find A(27),

`A(27)=27(108-2\cdot27)=27(108-54)=27\cdot54=1458`

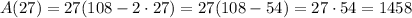
Hence, the maximum area is 1458 square feet.