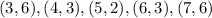Question

I need 5 points. the vertex, 2 to the left, and 2 to the right

Answer 1

Graph the parabola

`\begin{gathered} y=x^2-10x+27 \\ f(x)=ax^2+bx+c \end{gathered}`

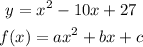
In order to find the vertex (h,k), we can use this formula

`\begin{gathered} h=(-b)/(2a) \\ k=f(h) \end{gathered}`

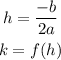
where,

a = 1

b = -10

c = 27

then, the vertex (h,k) is

`\begin{gathered} h=-(-10)/(2\cdot1)=(10)/(2)=5 \\ k=f(5)=5^2-10\cdot5+27=25-50+27=2 \end{gathered}`

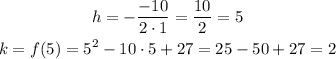
Therefore, vertex is the point (h,k) = (5,2)

Now, we just need two points to the left and two points to the right of this point

for example, when x = 3, then y = 6

`f(3)=3^2-10\cdot\: 3+27=6`

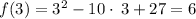
when x = 4, then y = 3

`f(4)=4^2-10\cdot\: 4+27=3`

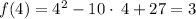
when x = 6, then y = 3

`f(6)=6^2-10\cdot\: 6+27=3`

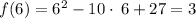
when x = 7, then y = 6

`f(7)=7^2-10\cdot\: 7+27=6`

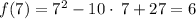
Thus, the set of 5 points is the following:

`(3,6),(4,3),(5,2),(6,3),(7,6)`