Answer:
D. The system is inconsistent
Explanation:
Given the below system of equations;
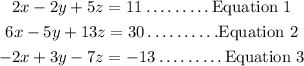
We'll follow the below steps to solve the above system of equations;
Step 1: Add Equation 1 and Equation 3;
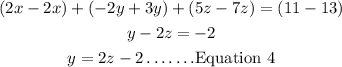
Step 2: Multiply Equation 3 by 3, we'll have;
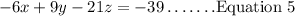
Step 3: Add Equation 2 and Equation 5, we'll have;

Step 4: Put Equation 4 into Equation 6 and solve for z;
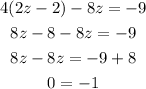
From the above, we can see that we do not have a solution for z, therefore, we can say that the system of equations has no solution, hence, it is inconsistent.