Question

A 1,982-kg car starts from rest at the top of a driveway 6.74 m long that is sloped at an angle of 30 degrees with the horizontal. If an average friction force of 2,721 N impedes the motion of the car, find the speed (in m/s) of the car at the bottom of the driveway.Use the approximation that g ≈ 10 m/s2.

Answer 1

In this situation, we cannot apply the law of conservation of energy, as there is friction. For us to solve, let us start by writing the balance equations. We'll have:

`\sum F_x=P*sin(30)-Fat=ma`
`\sum F_y=N-P*cos(30)=0`

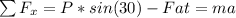
In order to find out the acceleration, we can use the first equation:

`a=(P*sin(30)-Fat)/(m)=(1982*10*sin(30)-2721)/(1982)=3.627(m)/(s^2)`

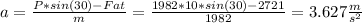
The car will then suffer this acceleration on the sloped plane. With this, we can calculate its speed by the end using the equations for a uniformly accelerated movement:

`S(t)=S_0+v_0t+(at^2)/(2)\Rightarrow6.74=(3.627*t^2)/(2)\Rightarrow t=1.928s`

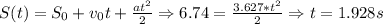
This is the time the car will take to reach the bottom. By replacing this on the equation for the velocity we get:

`v(t)=v_0+at=0+3.627*1.928=7(m)/(s)`

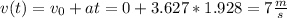
Then, our final answer is 7 m/s