When you roll a six-sided number cube you can get the next set of possible results:
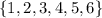
You have a total of 6 possible results.
From the set of possible results you get the set of presults that are 1 or 6:
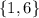
You have 2 results that are 1 or 6
The probability of rolling (1 or 6) is: The number of results that are 1 or 6 divided in the total number of possible results:
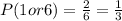
Then, the probability of rolling (1 or 6) is 1/3