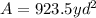We know the area of a cirlce is
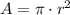
This is because, in radians, the angle of a whole circle is
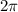
In order to proceed, we'll use the formula
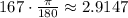
Using this new value, we can now compute the area of the shaded region using the formula
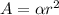
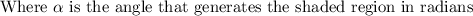
In this case we have:
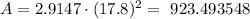
Round to the nearest tenth: