Given function:
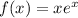
The minimum value of the function can be found by setting the first derivative of the function to zero.
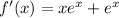
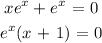
Solving for x:
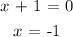
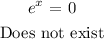
Substituting the value of x into the original function:
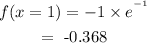
Hence, the minimum value in the given range is (-1, -0.368)