Question

A local health clinic surveys its patients about their water drinking habits it found data is normally distributed the mean amount of water consumed daily is 62 ounces and the standard deviation is 5.2how much water in ounces do approximately 95% of the patients drink each day

Answer 1

The approximate amount of water consumed by 95% of the patients will be given as a range which can be gotten by

`P=x\pm2S`

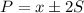
Where

P = Amount of water.

x = mean

S = Standard Deviation

Therefore,

The lower limit is

`\begin{gathered} x-2s \\ =62-2(5.2) \\ =62-10.4 \\ =51.6\text{ ounces} \end{gathered}`

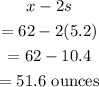
The upper limit is

`\begin{gathered} x+2s \\ =62+2(5.2) \\ =62+10.4 \\ =72.4\text{ ounces} \end{gathered}`

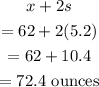
Therefore, the amount of water that 95% of the patients drink approximately is 51.6 ounces to 72.4 ounces.