A generic expression of a quadratic is

We can write it using the vertex form, that is

The vertex form holds a lot of important properties because it shows us immediately where the vertex is, just by looking at the value of "h" and "k" of the formula, in fact, the vertex of the parabola is
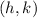
And the axis of symmetry of a parabola is the x-coordinate of the vertex, then, the axis of symmetry is
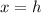
But how to identify h and k when we have the parabola in the vertex form? We have the following equation
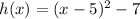
What's the value of the number that sums or subctract the quadratic term? In that case, it's -7, then it's the value of k
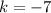
Now to identify the "h" we must take care, it seems like h = -5 because the quadratic term is (x-5)² but we always change the signal of the number inside the quadratic term, if we have -5 inside it, the value of h is 5
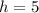
Then, the vertex will be
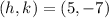
The vertex is (5, -7) and the axis of symmetry will be the same value of h, then

Symmetry and vertex
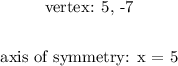
Now, to plot the graph precisely we must find the roots of the parabola, in other words, the value of x that makes h(x) equal to zero:
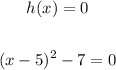
Then, we want to solve:
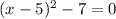
Put the quadratic term on one side
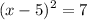
Take the square root on both sides
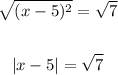
Be careful! when we do the square root of the quadratic term we must remember to put the modulus. Then we will solve this modular equation:
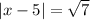
Which is the same as solving to different equations:

Then the two solutions are
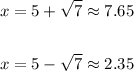
Then we can do the plot of the parabola with a good precision
Or using a graphing calculator