Question

Find the center and radius of the circle: x² + y² - 2x + 4y = -1

Answer 1

We need to complete the perfect square in x and y, that is,

`x^2-2x=(x-1)^2-1`

and

`y^2+4y=(y+2)^2-4`

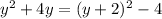
Then, our given equation can be rewritten as:

`(x-1)^2-1+(y+2)^2-4=-1`

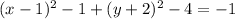
which is equal to

`\begin{gathered} (x-1)^2+(y+2)^2-5=-1 \\ \end{gathered}`

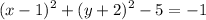
By moving -5 to the right hand side, we have

`\begin{gathered} \mleft(x-1\mright)^2+\mleft(y+2\mright)^2=-1+5 \\ \mleft(x-1\mright)^2+\mleft(y+2\mright)^2=4 \\ \mleft(x-1\mright)^2+\mleft(y+2\mright)^2=2^2 \end{gathered}`

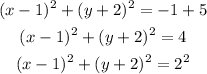
Since the general circle equation is

`\mleft(x-h\mright)^2+\mleft(y-k\mright)^2=r^2`

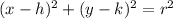
then, the answer is:

`(x-1)^2+(y+2)^2=2^2`

then, the center is (h,k)= (1, -2) and the radius is r=2