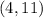
Step-by-step explanation
In geometry, the midpoint is the middle point of a line segment. It is equidistant from both endpoints
it is given by
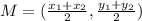
then
Step 1
Let
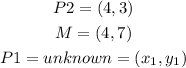
replace
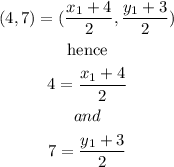
Step 2
now, we have to solve for x1 and y1
a)
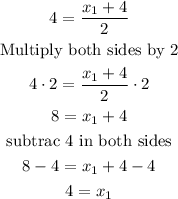
b)
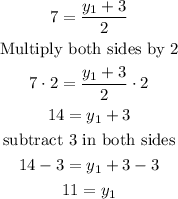
therefore, the coordinates of the other end point is
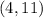
I hope this helps you