First we need to factorate the number 40:
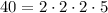
The possible numbers we can create using these factors are 2, 4, 5, 8, 10 and 20.
So If the product of the two factors (let's call them 'a' and 'b') is 40 and the sum is 14, we have:
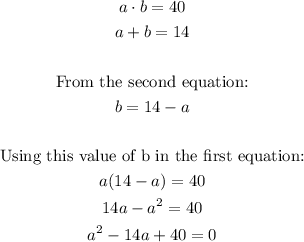
Using the quadratic formula to solve this equation, we have:
![\begin{gathered} a_1=\frac{-b+\sqrt[]{b^2-4ac}}{2a}=\frac{14+\sqrt[]{196-160}}{2}=(14+6)/(2)=10 \\ a_2=\frac{-b-\sqrt[]{b^2-4ac}}{2a}=(14-6)/(2)=4 \\ \\ a=10\to b=14-10=4 \\ a=4\to b=14-4=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/egl8r2xv3xhw0vrx957ib3tj3whz36kppd.png)
So the factors which product is 40 and the sum is 14 are 4 and 10.