To determine which option is correct, we first need to find the volume of both chocolate.
The volume of X:
The shape is a square-based pyramid. The volume is given by
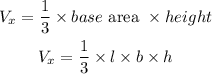
From the diagram,
l = 5 cm
b = 6 cm
h = 10 cm
Substituting,
![\begin{gathered} V_x=(1)/(3)*5*6*10 \\ V_x=100\operatorname{cm}^3 \end{gathered}]()
The volume of Y:
The shape is a triangular-based pyramid. The volume is given by
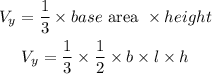
From the diagram,
l = 8 cm
b = 7.5 cm
h = 10 cm
![\begin{gathered} V_y=(1)/(3)*(1)/(2)*7.5*8*10 \\ V_y=100\operatorname{cm}^3 \end{gathered}]()
From here, the volumes of both chocolates are the same.
Therefore, the chocolate he picks does not matter as both volumes are equivalent.
The SECOND OPTION is correct.