SOLUTION
Given the question in the image, the following are the solution steps to answer the question.
STEP 1: Write the given coordinates
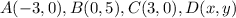
STEP 2: State the side properties of a rhombus
In a rhombus, all sides are equal. This means that the length of the sides are equal and therefore the distances of the vertices apart will be the same.
And also, Diagonals of rhombus bisect each other. This implies that:
Co-ordinates of mid-points of AC= Co-ordinates of mid-points of BD
STEP 3: Find the distances of the sides
Midpoints of AC will be calculated as:
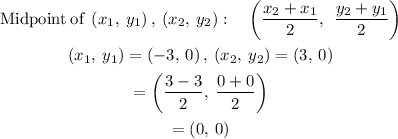
Midpoints of BD will be calculated as:
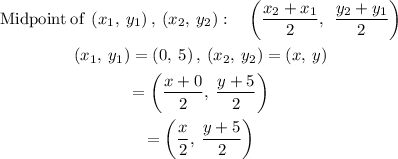
Since midpoints are the same as mentioned above, this means that:
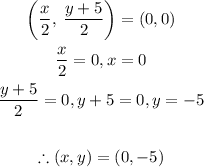
Hence, the coordinates of the fourth vertex is given as:
