PART A:
Let the number of days be represented by t. Let the total cost be represented by C.
FOR COMPANY A:
The equation to represent the total charges will be given as
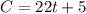
FOR COMPANY B:
The equation to represent the total charges will be given as
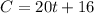
PART B:
Company B will charge less over a 9-day rental period.
To confirm this answer, we will calculate the cost using the equations derived above:
FOR COMPANY A:
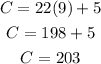
FOR COMPANY B:
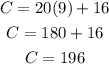
Therefore, COMPANY B will charge less over 9 days.
PART C:
To know how much is saved over a 15-day period, we will first calculate the cost of both companies over the period using the equations derived from Part A.
FOR COMPANY A:
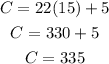
FOR COMPANY B:
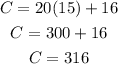
We can, thus, calculate the difference as
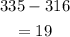
Therefore, the amount saved will be $19 over 15 days.