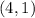Question

One equation from a system of two linear equations is graphed on the coordinate grid. 51 46 5 4 3 2 1 6 x -1 -21 The second equation in the system of linear equations has a slope of 3 and passes through the point (2,-5). What is the solution to the system of equations? th

Answer 1

First, we need to find the equation for the two equations.

The equation graphed has a y-intercept of 3 and a slope of

`m=(-6)/(3)=-3`

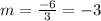
therefore, the equation of the line is

`\boxed{y=-(1)/(2)x+3.}`

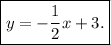
For the second equation, we know what it has a slope of 3; therefore it can be written as

`y=3x+b`

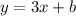
Now, we also know that this equation passes through the point y = -5, x = 2; therefore,

`-5=3(2)+b`

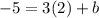
which gives

`-5=6+b`
`b=-11`

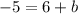
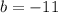
Hence, the equation of the line is

`\boxed{y=3x-11}`

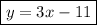
Now we have the equations

`\begin{gathered} y=-(1)/(2)x+3 \\ y=3x-11 \end{gathered}`

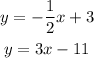
equating them gives

`-(1)/(2)x+3=3x-11`

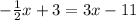
adding 11 to both sides gives

`-(1)/(2)x+14=3x`

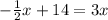
adding 1/2 x to both sides gives

`14=(7)/(2)x`

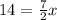
Finally, dividing both sides by 7/2 gives

`\boxed{x=4\text{.}}`

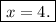
The corresponding value of y is found by substituting the above value into one of the equations

`y=-(1)/(2)(4)+3`
`y=1`

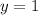
Hence, the solution to the system is

`(4,1)_{}`