We have the next equation
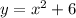
First, we need to find the focus of this parabola the vertice is in (0,6)
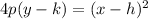
where in our case h =0, k=6
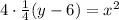
Therefore the focus will be
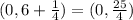
Then for Latus Rectum is located between the next points
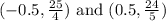
the latus Rectum
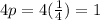
the length of the latus rectum is 1