ANSWER:
911.6 ft
Step-by-step explanation:
Given:
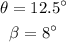
To find:
The distance between the two ships
Let's go ahead and draw a sketch as seen below;
Let's go ahead and solve for the value of AC by taking the tangent of angle 12.5 degrees as seen below;
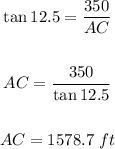
Let's now solve for the value of AD by taking the tangent of angle 8 degrees as seen below;
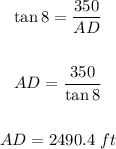
Therefore the distance between the two ships will be;
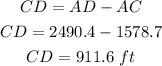
So the two ships are 911.6 ft