Answer:
y=2x+8
Explanation:
Given the two points:
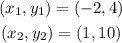
In order to find the equation of the line connecting them, we employ the use of the two-points formula given below:
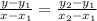
Substitute the values:
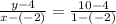
Next, simplify:
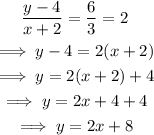
The equation containing the points (-2,4) and (1,10) is y=2x+8.