The free body diagram in shown below:
From the diagram and the problem we have that:
• The weight and angle of the inclined plane are given.
,
• The normal force and the components of the weight are unknown (this implies that the acceleration is unknown too); we also notice that the mass is not given the it is also an unknown.
We know that Newton's second law states that:
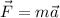
where F is the resultant force and a is the acceleration. Since this is a vector equation we can decomposed it in two scalar equations (in this case we only need two scalar equations since the forces are coplanar), then we have:

Since we don't expect the cyclist to move in the y direction (otherwise he will surely fall) the equations above would reduce to:
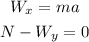
From the first equation we can solve the acceleration, to do this we use the triangle to get the x-component of the weight:
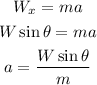
Since the weight is given but not the mass we use the fact that the weight is:
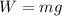
to get the mass, then we have:
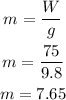
hence the mass of the cylcist is 7.65 kg.
Now that we have all the values we need we plug them in the expression for the acceleration:
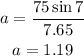
Therefore the acceleration of the cyclist is 1.19 meters per second per second.