Let 'x' be the number of calories per cup of popcorn, and 'y' be the number of calories per ounce of soda.
Given that 3 cups of popcorn and 6 oz of soda constitute 246 calories,
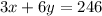
Also given that 1 cups of popcorn and 14 oz of soda constitute 274 calories,
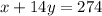
Solve the equations using Elimination Method.
Subtract 3 times equation 2 from equation 1,
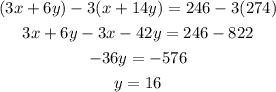
Substitute this value in equation 1, to obtain 'x' as,
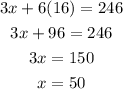
Thus, the solution of the system of equations is x=50 and y=16.
Therefore, there are 50 calories per cup of popcorn, and 16 calorie per ounce of soda.