Given:
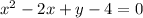
Let's complete the square to find the vertex of the parabola.
To solve first move all terms not containing y to the right side of the equation:
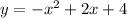
Now, take the vertex form of a parabola:
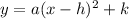
Apply the standard form of a parabola:
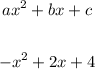
Thus, we have:
a = -1
b = 2
c = 4
Now, to find the value of h, we have:
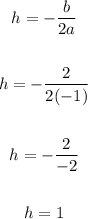
To find the value of k, we have:
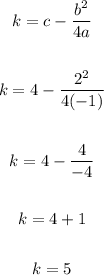
We have the values:
h = 1
k = 5
The vertex of the parabola is:
(h, k) ==> (1, 5)
ANSWER:
(1, 5)