Question

Suppose z varies directly with x and inversely with the square of y. If z = 18 when I = 6 and y = 2, what is z when I 7 and y = 7? Z =

Answer 1

It is given that z varies directly with x and inversely with the square of y so it follows:

`z=k(x)/(y^2)`

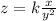
It is also given that z=18 when x=6 and y=2 so it follows:

`\begin{gathered} 18=k(6)/(2^2) \\ k=(18*4)/(6) \\ k=12 \end{gathered}`

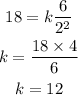
So the equation of variation becomes:

`z=12(x)/(y^2)`

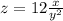
Therefore the value of z when x=7 and y=7 is given by:

`\begin{gathered} z=(12*7)/(7^2) \\ z=(12)/(7) \\ z\approx1.7143 \end{gathered}`

Hence the value of z is 12/7 or 1.7143.