Given:
Two circuits with multiple resistors
To find:
The net resistance of the circuits
Step-by-step explanation:
For the first circuit
The equivalent series resistance of the 1 and 2 is,
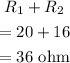
The equivalent series resistance of the 4 and 5 is,
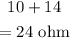
The net resistance of the resistances is,
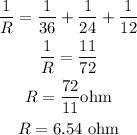
Hence, the net resistance of the upper circuit is 6.54 ohms.
For the circuit below:
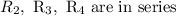
So, the equivalent resistance is,
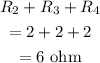
This equivalent resistance in parallel with
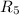
So, the equivalent resistance is,
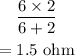
Now 1.5 ohm is in series with the rest two resistances.
So, the net resistance is,
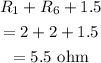
Hence, the net resistance of the circuit below is 5.5 ohms.