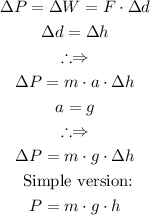Question

Derive Kinetic Energy and Potential Energy.

Answer 1

`\begin{gathered} \Delta K=(1)/(2)m(v_f)^2-(1)/(2)m(v_i)^2 \\ P=m\cdot g\cdot h \end{gathered}`

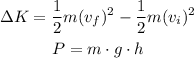
Step-by-step explanation: We need to derive the formula for both Kinetic energy and potential energy, the derivation of these formulas is as follows:

(i) Kinetic energy:

`\begin{gathered} \Delta K=\Delta W=F\cdot\Delta d\cdot\cos (\theta) \\ \theta=0 \\ \therefore\Rightarrow \\ \Delta K=F\cdot\Delta d\Rightarrow(1) \end{gathered}`

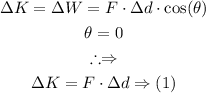
By using the Kinematic equations of motions, equation (1) can be changed to the kinetic energy formula as follows:

`\begin{gathered} (1)\Rightarrow\Delta K=F\cdot\Delta d=m\cdot a\cdot\Delta d\Rightarrow(2) \\ (v_f)^2=(v_i)^2+2a\Delta d \\ \therefore\Rightarrow \\ a\Delta d=((v_f)^2-(v_i)^2)/(2) \\ \text{ Substituting above in the }(2)\text{ gives the formula:} \\ \Delta K=m\cdot((v_f)^2-(v_i)^2)/(2) \\ \Delta K=(1)/(2)m(v_f)^2-(1)/(2)m(v_i)^2 \\ \text{ This is the kinetic energy formula} \end{gathered}`

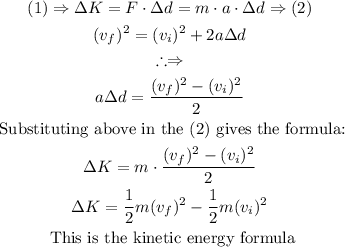
(ii) Potential-energy:

Potential energy is basically the work needed to lift an object to a certain height, mathematically, the derivation would be as follows:

`\begin{gathered} \Delta P=\Delta W=F\cdot\Delta d \\ \Delta d=\Delta h \\ \therefore\Rightarrow \\ \Delta P=m\cdot a\cdot\Delta h \\ a=g \\ \therefore\Rightarrow \\ \Delta P=m\cdot g\cdot\Delta h \\ \text{ Simple version:} \\ P=m\cdot g\cdot h \end{gathered}`