EXPLANATION :
From the problem, we have a linear function :
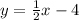
We need 2 points to graph this function.
when x = 0 :
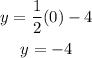
when x = 2
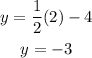
Plot the points (0, -4) and (2, -3)
Since the function is a continuous line, the domain and range are all real numbers.
Domain = (-∞, ∞)
Range = (-∞, ∞)
and since the graph is a line with a defined slope, this is a function