Question

Find the sum of all multiples of 7 between 1 to 200, inclusive.

Answer 1

2842

Step-by-step explanation:

The first multiple of 7 =7

The last multiple of 7 before 200 = 196

This problem forms an arithmetic sequence where:

• The first term, a= 7

,

• The last term, l = 196

To determine the sum, we find first the number of multiples of 7 between 7 and 196.

`\begin{gathered} \text{Number of multiples=}(196)/(7) \\ =28 \end{gathered}`

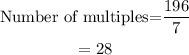
For a sequence with first and last terms, its sum is:

`\begin{gathered} S_n=(n)/(2)(a+l) \\ =(28)/(2)(7+196) \\ =14*203 \\ =2842 \end{gathered}`

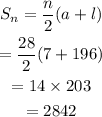
The sum of all multiples of 7 between 1 to 200 is 2842.

•