1.
The shelves can be assumed to be straight lines, and as straight lines have a 180° angle, then:

We know the value of m∠2. Thus, we can replace it and solve for m∠1:
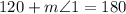
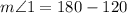

2.
If we can suppose that the top and middle shelves are cut by a transversal, then ∠1 and ∠5 are corresponding angles.
3.
When two parallel lines are cut by a transversal, they form corresponding angles, and these are equal in measure. Therefore, as:
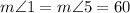
Then we can say that the top and middle shelves are parallel.
4.
As m∠11 = m∠2, we can say that they are alternate exterior angles, which are formed when parallel lines are cut by a transversal. Therefore, the bottom shelf is parallel to the top shelf.
5.
Finally, we can see that as m∠11 = 120°, we are in the same situation as in question 1, for which we conclude that m∠9 = 60°. Now, we have the same situation as in question 2, in which m∠5 and m∠9 are corresponding. Thus the bottom shelf is parallel to the middle shelf.