To solve this problem, we have to use conservation of momentum, which states that the initial momentum is equal to the final momentum. We know that momentum is defined as
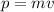
Let's apply it to the problem
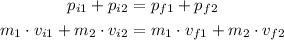
Using all the given information, we have
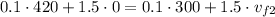
Now, we solve the equation for v_f2:
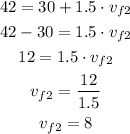
Hence, the target is moving 8 m/s after the collision.