Question

Write the slope-intercept form of the equation of the line described. 11.) through: ( 1 , 2 ) , perpendicular to Y= -1/5x +2

Answer 1

We would like to find the equation of the line that passes through the point (1.2) and is perpendicular to the line y=-1/5 x +2, and write in slope intercept form. To do this first we have to remeber that the equation of a line is given by

`y-y_1=m(x-x_1)`

and that to find it we need a point and the slope. In this case we have the point but we don't know the slope yet. To find the slope we notice that the line has to be perpendicular to the line y=-1/5 x +2. We need to remember that two lines are perpendicular if and only if

`m_1m_2=-1`

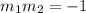
where m1 and m2 are the slopes of the lines.

The line y=-1/5 x +2 is wirtten in the slope-intercept form:

`y=mx+b`

from this we notice that its slope is -1/5, then using the relation for perpendicular lines we have that

`(-(1)/(5))(m)=-1`

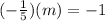
Solving for m we have that

`\begin{gathered} m=(-1)/(-1)(5) \\ =5 \end{gathered}`

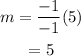
So, our line passes through the point (1,2) and has an slope equal to 5. Plugging this values on the equation for a line we have

`\begin{gathered} y-2=5(x-1) \\ y-2=5x-5 \\ y=5x-5+2 \\ y=5x-3 \end{gathered}`

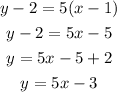
so the equation of the line we were looking for is y=5x-3. (Notice that it is already written in the adequate form).