1 Answer

Ask a Question

Erdinc · Answer 1 · 2023-06-10T14:26:24+0000

We are given the following uniform distribution:

The probability that the absolute value of the number is in the following interval:

$\begin{gathered} -7The probability is the area under the curve of the distribution. Therefore, we need to add both areas. The height of the distribution is:[tex]H=(1)/(b-a)$

Where:

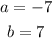
$\begin{gathered} a=-7 \\ b=7 \end{gathered}$

Substituting we get:

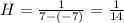
Therefore, the areas are:

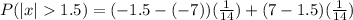
$P(\lvert x\rvert>1.5)=(-1.5-(-7))((1)/(14))+(7-1.5)((1)/(14))$

Simplifying we get:

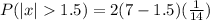
$P(\lvert x\rvert>1.5)=2(7-1.5)((1)/(14))$

Solving the operations:

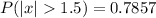
$P(\lvert x\rvert>1.5)=0.7857$

Therefore, the probability is 0.7857 or 78.57%.

A random number generator is programmed to produce numbers with a Unif (−7,7) distribution-example-1

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions