Question

Use the formula d = vt + 1672, where d is the distance in feet, v is the initial velocity in feet per second, and t is the time in seconds.An object is released from the top of a building 320 ft high. The initial velocity is 16 ft/s. How many seconds later will the object hit the ground?

Answer 1

We got to use the given formula:

`d=v\cdot t+16t^2`

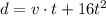
The distance, d, given is 320 ft and the initial velocity, v, 16 ft/s. We want the time, t. So:

`\begin{gathered} d=v\cdot t+16t^2 \\ 320=16t+16t^2 \\ 16t^2+16t-320=0 \\ (16t^2)/(16)+(16t)/(16)-(320)/(16)=(0)/(16) \\ t^2+t-20=0 \end{gathered}`

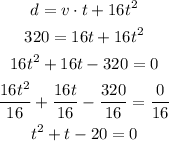
Now, we have a quadratic equation, so we can use Bhaskara formula:

`\begin{gathered} t=\frac{-1\pm\sqrt[]{1^2-4\cdot1\cdot(-20)}}{2\cdot1}=\frac{-1\pm\sqrt[]{1+80}}{2}=\frac{-1\pm\sqrt[]{81}}{2}=(-1\pm9)/(2) \\ t_1=(-1-9)/(2)=-(10)/(2)=-5 \\ t_2=(-1+9)/(2)=(8)/(2)=4 \end{gathered}`

Because we can't have a negative time, we consider only the second one, which it t = 4s.