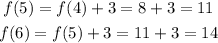Question

Two consecutive terms in an ARITHMETIC sequence are given. Find the recursive function.

Answer 1

An arithmetic sequence is a sequence of numbers such that the difference between the consecutive terms is constant.

The recursive formula have the following format:

`a_(n+1)=a_n+d`

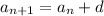
Where 'd' is the common difference between each term.

From the text, we know that

`\begin{gathered} a_3=5 \\ a_4=8 \end{gathered}`

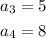
Plugging those values in our formula, we find that the common difference between our terms is 3.

This gives us the following recursive function:

`f(n+1)=f(n)+3`

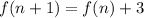
Evaluating the function at '5' and '6', we get the following:

`\begin{gathered} f(5)=f(4)+3=8+3=11 \\ f(6)=f(5)+3=11+3=14 \end{gathered}`