1 Answer

David Narayan · Answer 1 · 2023-12-29T11:42:04+0000

In order to find the area of the sector, let's consider the formula for the area of a circle:

$A=\pi r^2$

The complete circle is equivalent to a sector with central angle 2pi. Knowing this, we can write the following rule of three:

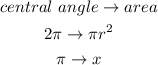
$\begin{gathered} central\text{ }angle\rightarrow area \\ 2\pi\rightarrow\pi r^2 \\ \pi\rightarrow x \end{gathered}$

Now, we can write the following proportion and solve it for x:

$\begin{gathered} (2\pi)/(\pi)=(\pi r^2)/(x)\\ \\ 2x=\pi r^2\\ \\ x=(\pi r^2)/(2)=(\pi\cdot0.7^2)/(2)=0.77\text{ in^^b2} \end{gathered}$

Therefore the area is 0.77 in².

Please log in or register to add a comment.