We are given the following information
Deposited amount = P = $9000
Interest rate = r = 6.6% = 0.066
Compounding interval = n = quarterly = 4
Number of years = t = 13
We are asked to find the accumulated amount (or ending balance)
Recall that the compound interest formula is given by
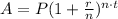
Where
A = Accumulated amount (or ending balance)
P = Deposit amount
r = Interest rate in decimal
n = Number of compounding in a year
t = Number of years
Now let us substitute the given values into the above formula
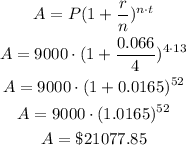
Therefore, after 13 years, the account balance will be $21077.85