Question

Solve the system of equations:3x+y=6 2x+3y=11

Answer 1

(1,3)

Explanation:

Given the system of equations:

`f(x)=\begin{cases}3x+y=6 \\ 2x+3y=11\end{cases}`

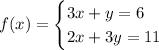
To solve the system using the elimination method, multiply the first equation by 3.

`\begin{gathered} f(x)=\begin{cases}9x+3y=18 \\ 2x+3y=11\end{cases} \\ \text{Subtract} \\ 7x=7 \\ \text{Divide both sides by 7} \\ (7x)/(7)=(7)/(7) \\ x=1 \end{gathered}`

Next, substitute x=1 into any of the equations to solve for y.

`\begin{gathered} 3x+y=6 \\ 3(1)+y=6 \\ y=6-3 \\ y=3 \end{gathered}`

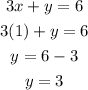
The solution to the system of equations is (x,y)=(1, 3).