Answer:
1287
Step-by-step explanation:
The number of distinct ways n objects can b selected from N total objects is given by
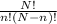
Now in our case, we have a total of 13 basketball players. N = 13 and 5 players to choose n = 5. Therefore, the above formula gives
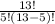
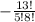
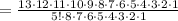

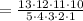
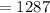
Hence, there are 1287 ways 5 different players can be selected from 13 players.