Question

Which best represents the transformations for the coordinates of the verticals of the given pairs of triangles (1,6), (-1,3), (5,2), and (-1,6), (-3,3), (3,2) Is it a rotation (that my educated guess)Reflection or translation?

Answer 1

No. It's not a rotation. It's translation.

for translation, there is a formula that is

`x^(\prime)=x+a\text{ }`

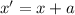
and

`y^(\prime)=b+y`
`y^(\prime)=b+y`

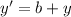
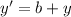
where (x',y') is the new coordinate and (x,y) is the old one and (a,b) is the increasing value of (x,y)

so here we have the new coordinates are (-1,6), (-3,3), (3,2)

and the olds are (1,6), (-1,3), (5,2)

`\begin{gathered} -1=a+1 \\ and\text{ }6=b+6 \\ this\text{ gives } \\ a=(-2)\text{ and b=0} \\ similarly\text{ you take each case you will get the value of a is \lparen-2\rparen and the value of b is 0.} \end{gathered}`

Thus we can say that the triangle is translated by adding the horizontal value (a) =(-2) to the x-coordinate of each vertex and the vertical value (b)=0 to the y-coordinate.

now you can see

`\begin{gathered} 1+(-2)=1\text{ \& 6+\lparen0\rparen=6 ie \lparen1,6\rparen+\lparen-2,0\rparen=\lparen-1,6\rparen} \\ similarly \\ (-1,3)+(-2,0)=(-3,3) \\ (5,2)+(-2,0)=(3,2) \end{gathered}`

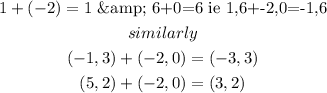
so the right answer is translation.